The three most common artifact types in RR time series are extra, missed, and ectopic beats, which generate short, long, and the sequences of short and long beat interval values, respectively [1].

Automatic approaches for the detection of erroneous beats can be divided into two categories, statistical methods and modeling-based approaches, which we will focus on [2]. However, the detection accuracies of statistical methods are poor when compared to modeling-based approaches. The modeling approaches have typically higher time complexity and their implementation is often difficult.

To construct a model of the expected dynamics for different rhythms and compare the observed signal (or derived features) to this model. Such model-based approaches can be RR interval statistics-based methods.

Ectopic beats are defined (in terms of timing) as those which have intervals less than or equal to 80% of the previous sinus cycle length. The obvious choice for spectral estimation for HRV is therefore the removal of up to 20% of the data points in an RR time series without introducing a significant error in an HRV metric.

Example In adult human data, for example, if the current RR interval is 850 msec (70.6 bpm). the next RR interval may have an expected width ranging from 1125 msec {53.3 bpm) to 642 msec (93.5 bpm) and the algorithm will still be capable of detecting the occurrence of either a type A or a type B error.

Therefore, if no morphological ECG is available, and only the RR intervals are available, it is appropriate to employ an aggressive beat removal scheme (removing any interval that changes by more than 12.5% on the previous interval) to ensure that ectopic beats are not included in the calculation. Of course, since the ectopic beat causes a change in conduction, and momentarily disturbs the sinus rhythm, it is inappropriate to include the intervals associated with the beats that directly follow an ectopic beat, and therefore, all the affected beats should be removed at this nonstationarity. As long as there is no significant change in the phase of the sinus rhythm after the run of affected beats, then we are safe. Otherwise, the time series should be segmented at the nonstationarity.

Fun fact In the following discussion, the term RR intervals will be reserved for the cardiac interbeat intervals between actual heartbeats. The term interevent interval will refer to the interval between recorded heartbeats which may or may not contain errors. Similarly, the symbol B will denote the actual RR interval, whereas the symbol B' will denote an erroneously recorded interevent interval [3].

Type A error

The threshold detector may prematurely trigger when an R-wave has not occurred. For the sake of convenience, this will be labeled a type A error. A type A error would in effect subdivide an RR interval into two consecutive interevent intervals, one or both of which will be exceptionally narrow compared to the other correctly recorded interbeat intervals.

Type B error

The threshold detector may fail to trigger with the occurrence of an R-wave. Again, for the sake of convenience, this will be labeled a type B error. A type B error would result in two consecutive RR intervals being merged and recorded as an exceptionally wide interevent interval.

Type C error

Note that this discussion assumes that the error is only possible on the sensor trigger detection, but it can be that there is an error 'ectopic' beat at the heart muscles side. Such ectopic beat has different behavior in data and could be detected as well. Let's call it a Type C error. Type C errors are diverse ectopic beats that have their root cause in heart muscle problems, and not so much with the threshold detector of an ECG sensor. For this discussion, we have chosen Premature ventricular contractions (PVC), but take a look in figure for other types of ectopic beats.

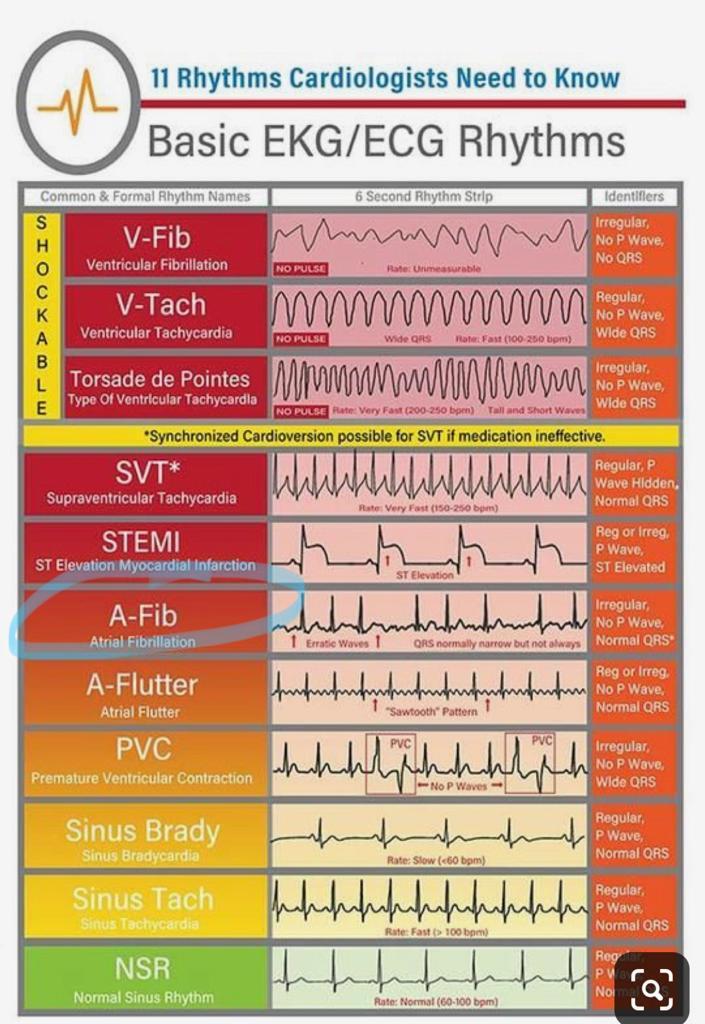
Acording to [4], the criteria for excluding PVCs must be stringent since HRT quantification can only deliver usable results if the triggering event was a true PVC (and not an artifact, T wave, or similar non-PVC event). In addition, the sinus rhythm immediately preceding and following the PVC must be checked to ensure that it is free from arrhythmia, artifacts, and false beat classifications due to artifacts. A useful set of exclusion criteria are:

1. Remove all RR intervals < 300 ms or > 2, 000 ms;
2. Remove all RRn where ||RRn−1 − RRn|| > 200 ms;
3. Remove all RR intervals that change by more than > 20% to the mean of the five last sinus intervals (the reference interval);
4. Only use PVCs with minimum prematurity of 20%;
5. Exclude PVCs with a postextrasystole interval that is at least 20% longer than the normal interval.

In PVC there occurs heart-rate turbulence, which is usually quantified by two numerical parameters: turbulence onset (TO) and turbulence slope (TS).

Turbulence onset

In the RR time series due to a PVC, note that the following beat after the PVC (RR+1) has an associated elongated RR interval, the compensatory pause after the early (premature) preceding beat.

TO is defined as the percentage difference between the average value of the first two normal RR intervals following the PVC (RRn, n = 2, 3) and of the last two normal intervals preceding the PVC (RR−n, n = 2, 1), where RR−2 and RR−1 are the first two normal intervals preceding the PVC and RR+2 and RR+3 the first two normal intervals following the PVC. (Note that there are two intervals associated with the PVC; the normal-PVC interval, RR0, and the following PVC-normal interval RR+1.) Therefore, positive TO values indicate deceleration and negative TO values indicate an acceleration of the post-ectopic sinus rhythm.

TO= ((RR+2 + RR+3) − (RR−2 + RR−1) / RR−2 + RR−1) × 100

Although the TO can be determined for each PVC (and should be if performed online), TO has shown to be more (clinically) predictive if the average value of all individual measurements is calculated. For the calculation of the mean TO, at least 15 normal intervals after every single PVC are required.

TO values below 0 and TS values above 2.5 are considered normal, and abnormal otherwise (i.e., a healthy response to PVCs is a strong sinus acceleration followed by a rapid deceleration).

Turbulence slope

TS is calculated by constructing an average ectopy-centered time series32 and determining the steepest (linearly regressed) slope for each possible sequence of five consecutive normal intervals in the post-PVC “disturbed” time series (usually taken to be up to RR+16; the first 15 normal RR intervals). That is, all possible slopes from the set {RR+2,+3,...,+6, . . . , RR+17,+18,...,+16} are calculated, and the maximum of the 13 possible slopes is taken to be the TS. These values are usually averaged over all acceptable candidates and can run into the tens of thousands for 24-hour Holter recordings.

Heart-rate turbulence

Although the exact mechanism that leads to HRT is unknown, it is thought to be an autonomous baroreflex whereby the PVC causes a brief disturbance of arterial blood pressure. Therefore, HRT can be measured around the point of atrial ectopy as well as ventricular ectopy. When the autonomic control system is healthy, this rapid change causes an instantaneous response in the following RR intervals. If the autonomic control system is impaired, the magnitude of this response is either diminished or possibly completely absent.

From a clinical perspective, HRT metrics are predictive of mortality and possibly cardiac arrest. Furthermore, HRT metrics are particularly useful when the patients are taking beta-blockers. In a study, combined TO and TS was found to be the only independent predictor of mortality compared to otherwise predictive markers such as mean HR, previous myocardial infarction, and a low ejection fraction.

Detection of errors

Detection of errors is based on the assumption that the beat-to-beat variation in R-R intervals cannot exceed certain critical percentages of the preceding interval.

The error recovery process as illustrated in [3].

The detection of errors is intuitively simple: the condition is imposed that any interevent interval may not be wider nor narrower than the preceding interevent interval by certain critical percentages, otherwise the interevent interval in question is considered to be in error.

We are not able to modify the sensor embedded code, but biasing the threshold detector so that it will trigger at a slightly lower voltage level and/or slope than typical of a R~wave. This practice is to be recommended, in fact, for another advantage it offers.

With a type B error, the R-wave is lost and the R-R interval must be reconstructed, whereas with a type A error the R-wave is not lost and so the R-R interval merely has to be recovered. Thus, minimizing the occurrence of type B errors, even though it means increasing the likelihood of type A errors, actually maximizes the accuracy of the processed data.

Detection algorithm in RR time series

We will be following the method proposed by [1]. The algorithm is shown mathematically to be capable of detecting errors in data with extreme beat-to-beat variability. The basic algorithm is to compare each interevent interval to the preceding one. If the difference in width exceeds certain percentages, an error is detected.

• If type A error, that RR interval would be subdivided into two and recorded as the <i+1>th and <i+2>th interevent intervals.

• If a type B error has occurred at the <i+1>th R-wave, then the <i+1>th and the <i+2>th R-R tntervals would be merged and recorded as the <i+1>th interevent interval.

Correction of errors

Detected errors are corrected by merging the questionable interval with the preceding or the succeeding interval, or by subdividing it, in such a manner that the resultant beat-to-beat variability is minimized.

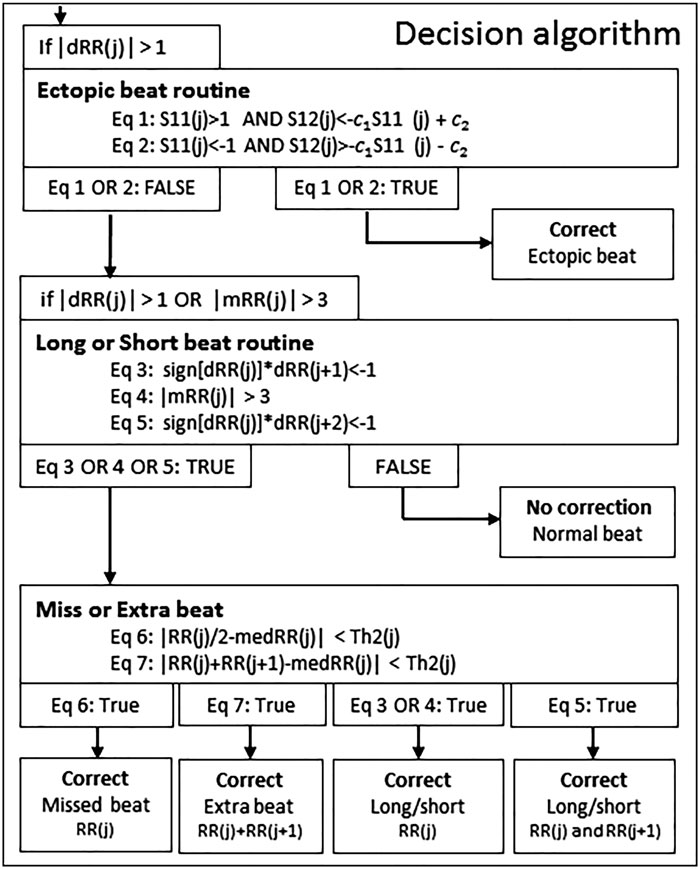The schematic presentation of the decision algorithm for detecting real artefacts and removing extra detection, as illustrated in [1].

Recovery of the actual RR interval is then attempted before comparison of further interevent intervals is to proceed; the recovery procedure consists of iteratively summing into or subdividing the interevent interval in question and comparing the outcome to the current preceding interevent interval until an acceptable reconstruction is achieved. Thus, assuming that the interevent interval used as the standard for the first comparison is not in error, the algorithm processes each consecutive interevent interval to correct detected errors and then uses the processed interevent interval as the standard for the next comparison.

Once an error is detected, however, any anomaly in the recovery procedure may compound the error, and when the erroneously corrected interval is used as a standard to screen the next interevent interval the effects of the anomaly may be propagated down the series of data, with possibly grave and drastic implications

Furthermore, errors tend to occur in bursts. It is not uncommon, for example, for the threshold detector to falsely trigger several times for a few consecutive RR intervals, producing a string of alternative corrections which appear equally plausible. Both of these problems must be dealt with in the recovery phase of error processing.

The original recorded RR time series (generated) that have all the mentioned artifacts, as illustrated by letters a, b, c respectively. The data comes from Brainjam app (Jamzone).

The corrected RR time series for ectopic beats (i.e., PVC), as illustrated by the letter c.

The corrected RR time series for missed beats, as illustrated by the letter b.

The corrected RR time series for extra beats, as illustrated by the letter a.

	Original	Removal	Correction
HR [bpm]	64	60	60
RMSSD	250	64	64
LF	6443	1986	2068
HF	9588	826	822

Two additional assumptions are made in the recovery procedure.

1. One of these states that the width of RR intervals tends to oscillate at about the same level. This is a straightforward and realistic assumption.
2. The other assumption states that the variability of a record of interevent intervals containing errors is greater than the variability of the corresponding RR intervals. provided that the fundamental assumption is not violated.

Although this assumption may easily be shown not to be true under all conditions, it does provide a systematic solution to the problem of multiple alternate plausible corrections when necessary. It should be noted that the researcher is frequently interested in the identification of responses in the data in the form of directional changes; in this regard, the assumption usually results in the most conservative alternative corrections to the data, since the minimization of beat-to-beat variation is a minimization of transient directional shifts. Nevertheless, directional responses which involve several beats are accurately retained if the majority of the beats are recorded without error.

Much of the error recovery procedure is modeled on an analysis of the hypothetical steps undertaken by a researcher manually correcting errors. The basic decision to be made is whether an interevent interval that has been deemed to be in error should be summed with either the preceding or the succeeding interval, and if neither, whether and how it should be subdivided. In the case of multiple errors within the same R-R interval, the recovery process proceeds in iterations. At each iteration, only one summing or subdivision is performed. The outcome is then compared against the preceding interval using the error detection procedure. If it is still in error, the recovery procedure is again invoked.

Recovery algorithm

First, two reference interevent intervals are selected where it is reasonably certain that no error has occurred, the first prior and the second after the questionable interval. Only the data exclusively between the two reference intervals can affect the variability of the corrected data as far as the current error is concerned, Therefore, only this data needs to be accounted for during the current recovery iteration.

Once the reference points are established, the effects on the variability of the data can be compared for three recovery alternatives:

1. merging the questionable interval with its preceding interval
2. merging the questionable interval with its succeeding interval
3. merging with neither

To estimate the variability of the data with the questionable interval and its preceding interval merged, the sum of all intervals following the first reference up to and including the questionable interval is subdivided into equal portions of width as close as possible to the first reference. The sum of all intervals following the questionable interval up to but excluding the second reference is similarly subdivided. An estimate of the variability is then provided by the sum of the absolute differences in width between the first reference and the first set of portions, between the two sets of portions, and between the second set and the second reference. The variability of the data with the questionable interval merged in the other direction is estimated in like manner. It can be shown that the

It can be shown that the expected difference between these two variability estimates is about two times the quotient of the width of the first reference divided by the total number of portions exclusively between the two references if a type A (false trigger) error has occurred, and about zero otherwise. Thus, if the actual difference exceeds the mean of these two expectancies, the questionable interval should be merged with a neighboring interval in the direction where the variability is minimized. Otherwise, it should be subdivided as appropriate.

The decision algorithm discriminates beats into different types of erroneous beats, which guides how the erroneous beat is corrected. A schematic presentation of the proposed decision algorithm is presented in Figure 1.

Limitations

This is not true, however, if the data contains complex errors such that both type A and type B errors occur within the same R-R interval; that is if a false trigger by the threshold detector is followed immediately by a failure to trigger or vice versa. In these cases, the algorithm becomes more effective in detecting complex errors as smaller critical percentages are used.